Mathematical Framework for latentcor

Mingze Huang, Christian L. Müller, Irina Gaynanova

2022-08-31

Latent Gaussian Copula Model for Mixed Data

latentcor utilizes the powerful semi-parametric latent Gaussian copula models to estimate latent correlations between mixed data types (continuous/binary/ternary/truncated or zero-inflated). Below we review the definitions for each type.

Definition of continuous model (Fan et al. 2017)

A random \(X\in\cal{R}^{p}\) satisfies the Gaussian copula (or nonparanormal) model if there exist monotonically increasing \(f=(f_{j})_{j=1}^{p}\) with \(Z_{j}=f_{j}(X_{j})\) satisfying \(Z\sim N_{p}(0, \Sigma)\), \(\sigma_{jj}=1\); we denote \(X\sim NPN(0, \Sigma, f)\).

X = gen_data(n = 6, types = "con")$X
X
#>             [,1]
#> [1,] -0.05894138
#> [2,]  0.61420386
#> [3,]  1.62989498
#> [4,]  1.34911221
#> [5,]  0.39471148
#> [6,] -0.32654291

Definition of binary model (Fan et al. 2017)

A random \(X\in\cal{R}^{p}\) satisfies the binary latent Gaussian copula model if there exists \(W\sim NPN(0, \Sigma, f)\) such that \(X_{j}=I(W_{j}>c_{j})\), where \(I(\cdot)\) is the indicator function and \(c_{j}\) are constants.

X = gen_data(n = 6, types = "bin")$X
X
#>      [,1]
#> [1,]    0
#> [2,]    0
#> [3,]    1
#> [4,]    1
#> [5,]    1
#> [6,]    0

Definition of ternary model (Quan, Booth, and Wells 2018)

A random \(X\in\cal{R}^{p}\) satisfies the ternary latent Gaussian copula model if there exists \(W\sim NPN(0, \Sigma, f)\) such that \(X_{j}=I(W_{j}>c_{j})+I(W_{j}>c'_{j})\), where \(I(\cdot)\) is the indicator function and \(c_{j}<c'_{j}\) are constants.

X = gen_data(n = 6, types = "ter")$X
X
#>      [,1]
#> [1,]    0
#> [2,]    2
#> [3,]    1
#> [4,]    1
#> [5,]    1
#> [6,]    0

Definition of truncated or zero-inflated model (Yoon, Carroll, and Gaynanova 2020)

A random \(X\in\cal{R}^{p}\) satisfies the truncated latent Gaussian copula model if there exists \(W\sim NPN(0, \Sigma, f)\) such that \(X_{j}=I(W_{j}>c_{j})W_{j}\), where \(I(\cdot)\) is the indicator function and \(c_{j}\) are constants.

X = gen_data(n = 6, types = "tru")$X
X
#>           [,1]
#> [1,] 1.1646683
#> [2,] 0.1497381
#> [3,] 0.0000000
#> [4,] 0.0000000
#> [5,] 0.0000000
#> [6,] 0.5315542

Mixed latent Gaussian copula model

The mixed latent Gaussian copula model jointly models \(W=(W_{1}, W_{2}, W_{3}, W_{4})\sim NPN(0, \Sigma, f)\) such that \(X_{1j}=W_{1j}\), \(X_{2j}=I(W_{2j}>c_{2j})\), \(X_{3j}=I(W_{3j}>c_{3j})+I(W_{3j}>c'_{3j})\) and \(X_{4j}=I(W_{4j}>c_{4j})W_{4j}\).

set.seed("234820")
X = gen_data(n = 100, types = c("con", "bin", "ter", "tru"))$X
head(X)
#>            [,1] [,2] [,3]      [,4]
#> [1,] -0.5728663    0    1 0.0000000
#> [2,] -1.5632883    0    0 0.0000000
#> [3,]  0.4600555    1    1 0.2634213
#> [4,] -1.5186510    1    1 0.0000000
#> [5,] -1.5438165    0    1 0.0000000
#> [6,] -0.5656219    0    0 0.0000000

Moment-based estimation of \(\Sigma\) based on bridge functions

The estimation of latent correlation matrix \(\Sigma\) is achieved via the bridge function \(F\) which is defined such that \(E(\hat{\tau}_{jk})=F(\sigma_{jk})\), where \(\sigma_{jk}\) is the latent correlation between variables \(j\) and \(k\), and \(\hat{\tau}_{jk}\) is the corresponding sample Kendall’s \(\tau\).

Kendall’s \(\tau\) (\(\tau_{a}\))

Given observed \(\mathbf{x}_{j}, \mathbf{x}_{k}\in\cal{R}^{n}\),

\[ \hat{\tau}_{jk}=\hat{\tau}(\mathbf{x}_{j}, \mathbf{x}_{k})=\frac{2}{n(n-1)}\sum_{1\le i<i'\le n}sign(x_{ij}-x_{i'j})sign(x_{ik}-x_{i'k}), \] where \(n\) is the sample size.

latentcor calculates pairwise Kendall’s \(\widehat \tau\) as part of the estimation process

estimate = latentcor(X, types = c("con", "bin", "ter", "tru"))
K = estimate$K
K
#>           [,1]      [,2]      [,3]      [,4]
#> [1,] 1.0000000 0.2557576 0.2456566 0.3331313
#> [2,] 0.2557576 1.0000000 0.1555556 0.2339394
#> [3,] 0.2456566 0.1555556 1.0000000 0.2183838
#> [4,] 0.3331313 0.2339394 0.2183838 1.0000000

Using \(F\) and \(\widehat \tau_{jk}\), a moment-based estimator is \(\hat{\sigma}_{jk}=F^{-1}(\hat{\tau}_{jk})\) with the corresponding \(\hat{\Sigma}\) being consistent for \(\Sigma\) (Fan et al. 2017; Quan, Booth, and Wells 2018; Yoon, Carroll, and Gaynanova 2020).

The explicit form of bridge function \(F\) has been derived for all combinations of continuous(C)/binary(B)/ternary(N)/truncated(T) variable types, and we summarize the corresponding references. Each of this combinations is implemented in latentcor.

Type continuous binary ternary zero-inflated (truncated)
continuous Liu, Lafferty, and Wasserman (2009) - - -
binary Fan et al. (2017) Fan et al. (2017) - -
ternary Quan, Booth, and Wells (2018) Quan, Booth, and Wells (2018) Quan, Booth, and Wells (2018) -
zero-inflated (truncated) Yoon, Carroll, and Gaynanova (2020) Yoon, Carroll, and Gaynanova (2020) See Appendix Yoon, Carroll, and Gaynanova (2020)

Below we provide an explicit form of \(F\) for each combination.

Theorem (explicit form of bridge function) Let \(W_{1}\in\cal{R}^{p_{1}}\), \(W_{2}\in\cal{R}^{p_{2}}\), \(W_{3}\in\cal{R}^{p_{3}}\), \(W_{4}\in\cal{R}^{p_{4}}\) be such that \(W=(W_{1}, W_{2}, W_{3}, W_{4})\sim NPN(0, \Sigma, f)\) with \(p=p_{1}+p_{2}+p_{3}+p_{4}\). Let \(X=(X_{1}, X_{2}, X_{3}, X_{4})\in\cal{R}^{p}\) satisfy \(X_{j}=W_{j}\) for \(j=1,...,p_{1}\), \(X_{j}=I(W_{j}>c_{j})\) for \(j=p_{1}+1, ..., p_{1}+p_{2}\), \(X_{j}=I(W_{j}>c_{j})+I(W_{j}>c'_{j})\) for \(j=p_{1}+p_{2}+1, ..., p_{3}\) and \(X_{j}=I(W_{j}>c_{j})W_{j}\) for \(j=p_{1}+p_{2}+p_{3}+1, ..., p\) with \(\Delta_{j}=f(c_{j})\). The rank-based estimator of \(\Sigma\) based on the observed \(n\) realizations of \(X\) is the matrix \(\mathbf{\hat{R}}\) with \(\hat{r}_{jj}=1\), \(\hat{r}_{jk}=\hat{r}_{kj}=F^{-1}(\hat{\tau}_{jk})\) with block structure

\[ \mathbf{\hat{R}}=\begin{pmatrix} F_{CC}^{-1}(\hat{\tau}) & F_{CB}^{-1}(\hat{\tau}) & F_{CN}^{-1}(\hat{\tau}) & F_{CT}^{-1}(\hat{\tau})\\ F_{BC}^{-1}(\hat{\tau}) & F_{BB}^{-1}(\hat{\tau}) & F_{BN}^{-1}(\hat{\tau}) & F_{BT}^{-1}(\hat{\tau})\\ F_{NC}^{-1}(\hat{\tau}) & F_{NB}^{-1}(\hat{\tau}) & F_{NN}^{-1}(\hat{\tau}) & F_{NT}^{-1}(\hat{\tau})\\ F_{TC}^{-1}(\hat{\tau}) & F_{TB}^{-1}(\hat{\tau}) & F_{TN}^{-1}(\hat{\tau}) & F_{TT}^{-1}(\hat{\tau}) \end{pmatrix} \] \[ F(\cdot)=\begin{cases} CC:\ 2\sin^{-1}(r)/\pi \\ \\ BC: \ 4\Phi_{2}(\Delta_{j},0;r/\sqrt{2})-2\Phi(\Delta_{j}) \\ \\ BB: \ 2\{\Phi_{2}(\Delta_{j},\Delta_{k};r)-\Phi(\Delta_{j})\Phi(\Delta_{k})\} \\ \\ NC: \ 4\Phi_{2}(\Delta_{j}^{2},0;r/\sqrt{2})-2\Phi(\Delta_{j}^{2})+4\Phi_{3}(\Delta_{j}^{1},\Delta_{j}^{2},0;\Sigma_{3a}(r))-2\Phi(\Delta_{j}^{1})\Phi(\Delta_{j}^{2})\\ \\ NB: \ 2\Phi_{2}(\Delta_{j}^{2},\Delta_{k},r)\{1-\Phi(\Delta_{j}^{1})\}-2\Phi(\Delta_{j}^{2})\{\Phi(\Delta_{k})-\Phi_{2}(\Delta_{j}^{1},\Delta_{k},r)\} \\ \\ NN: \ 2\Phi_{2}(\Delta_{j}^{2},\Delta_{k}^{2};r)\Phi_{2}(-\Delta_{j}^{1},-\Delta_{k}^{1};r)-2\{\Phi(\Delta_{j}^{2})-\Phi_{2}(\Delta_{j}^{2},\Delta_{k}^{1};r)\}\{\Phi(\Delta_{k}^{2})-\Phi_{2}(\Delta_{j}^{1},\Delta_{k}^{2};r)\} \\ \\ TC: \ -2\Phi_{2}(-\Delta_{j},0;1/\sqrt{2})+4\Phi_{3}(-\Delta_{j},0,0;\Sigma_{3b}(r)) \\ \\ TB: \ 2\{1-\Phi(\Delta_{j})\}\Phi(\Delta_{k})-2\Phi_{3}(-\Delta_{j},\Delta_{k},0;\Sigma_{3c}(r))-2\Phi_{3}(-\Delta_{j},\Delta_{k},0;\Sigma_{3d}(r)) \\ \\ TN: \ -2\Phi(-\Delta_{k}^{1})\Phi(\Delta_{k}^{2}) + 2\Phi_{3}(-\Delta_{k}^{1},\Delta_{k}^{2},\Delta_{j};\Sigma_{3e}(r))+2\Phi_{4}(-\Delta_{k}^{1},\Delta_{k}^{2},-\Delta_{j},0;\Sigma_{4a}(r))+2\Phi_{4}(-\Delta_{k}^{1},\Delta_{k}^{2},-\Delta_{j},0;\Sigma_{4b}(r)) \\ \\ TT: \ -2\Phi_{4}(-\Delta_{j},-\Delta_{k},0,0;\Sigma_{4c}(r))+2\Phi_{4}(-\Delta_{j},-\Delta_{k},0,0;\Sigma_{4d}(r)) \\ \end{cases} \]

where \(\Delta_{j}=\Phi^{-1}(\pi_{0j})\), \(\Delta_{k}=\Phi^{-1}(\pi_{0k})\), \(\Delta_{j}^{1}=\Phi^{-1}(\pi_{0j})\), \(\Delta_{j}^{2}=\Phi^{-1}(\pi_{0j}+\pi_{1j})\), \(\Delta_{k}^{1}=\Phi^{-1}(\pi_{0k})\), \(\Delta_{k}^{2}=\Phi^{-1}(\pi_{0k}+\pi_{1k})\),

\[ \Sigma_{3a}(r)= \begin{pmatrix} 1 & 0 & \frac{r}{\sqrt{2}} \\ 0 & 1 & -\frac{r}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & -\frac{r}{\sqrt{2}} & 1 \end{pmatrix}, \;\;\; \Sigma_{3b}(r)= \begin{pmatrix} 1 & \frac{1}{\sqrt{2}} & \frac{r}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & 1 & r \\ \frac{r}{\sqrt{2}} & r & 1 \end{pmatrix}, \;\;\; \Sigma_{3c}(r)= \begin{pmatrix} 1 & -r & \frac{1}{\sqrt{2}} \\ -r & 1 & -\frac{r}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{r}{\sqrt{2}} & 1 \end{pmatrix}, \]

\[ \Sigma_{3d}(r)= \begin{pmatrix} 1 & 0 & -\frac{1}{\sqrt{2}} \\ 0 & 1 & -\frac{r}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & -\frac{r}{\sqrt{2}} & 1 \end{pmatrix}, \;\;\; \Sigma_{3e}(r)= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & r \\ 0 & r & 1 \end{pmatrix}, \;\;\; \Sigma_{4a}(r)= \begin{pmatrix} 1 & 0 & 0 & \frac{r}{\sqrt{2}} \\ 0 & 1 & -r & \frac{r}{\sqrt{2}} \\ 0 & -r & 1 & -\frac{1}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & \frac{r}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 1 \end{pmatrix}, \]

\[ \Sigma_{4b}(r)= \begin{pmatrix} 1 & 0 & r & \frac{r}{\sqrt{2}} \\ 0 & 1 & 0 & \frac{r}{\sqrt{2}} \\ r & 0 & 1 & \frac{1}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & \frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 1 \end{pmatrix}, \;\;\; \Sigma_{4c}(r)= \begin{pmatrix} 1 & 0 & \frac{1}{\sqrt{2}} & -\frac{r}{\sqrt{2}} \\ 0 & 1 & -\frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{r}{\sqrt{2}} & 1 & -r \\ -\frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} & -r & 1 \end{pmatrix}\;\;\text{and}\;\; \Sigma_{4d}(r)= \begin{pmatrix} 1 & r & \frac{1}{\sqrt{2}} & \frac{r}{\sqrt{2}} \\ r & 1 & \frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{r}{\sqrt{2}} & 1 & r \\ \frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} & r & 1 \end{pmatrix}. \]

Estimation methods

Given the form of bridge function \(F\), obtaining a moment-based estimation \(\widehat \sigma_{jk}\) requires inversion of \(F\). latentcor implements two methods for calculation of the inversion:

Both methods calculate inverse bridge function applied to each element of sample Kendall’s \(\tau\) matrix. Because the calculation is performed point-wise (separately for each pair of variables), the resulting point-wise estimator of correlation matrix may not be positive semi-definite. latentcor performs projection of the pointwise-estimator to the space of positive semi-definite matrices, and allows for shrinkage towards identity matrix using the parameter nu (see Subsection describing adjustment of point-wise estimator and relevant parameter nu).

Original method (method = "original")

Original estimation approach relies on numerical inversion of \(F\) based on solving uni-root optimization problem. Given the calculated \(\widehat \tau_{jk}\) (sample Kendall’s \(\tau\) between variables \(j\) and \(k\)), the estimate of latent correlation \(\widehat \sigma_{jk}\) is obtained by calling optimize function to solve the following optimization problem: \[ \widehat r_{jk} = \arg\min_{r} \{F(r) - \widehat \tau_{jk}\}^2. \] The parameter tol controls the desired accuracy of the minimizer and is passed to optimize, with the default precision of 1e-8:

estimate = latentcor(X, types = c("con", "bin", "ter", "tru"), method = "original", tol = 1e-8)

Algorithm for Original method

Input: \(F(r)=F(r, \mathbf{\Delta})\) - bridge function based on the type of variables \(j\), \(k\)

  • Step 1. Calculate \(\hat{\tau}_{jk}\) using (1).
estimate$K
#>           [,1]      [,2]      [,3]      [,4]
#> [1,] 1.0000000 0.2557576 0.2456566 0.3331313
#> [2,] 0.2557576 1.0000000 0.1555556 0.2339394
#> [3,] 0.2456566 0.1555556 1.0000000 0.2183838
#> [4,] 0.3331313 0.2339394 0.2183838 1.0000000
  • Step 2. For binary/truncated variable \(j\), set \(\hat{\mathbf{\Delta}}_{j}=\hat{\Delta}_{j}=\Phi^{-1}(\pi_{0j})\) with \(\pi_{0j}=\sum_{i=1}^{n}\frac{I(x_{ij}=0)}{n}\). For ternary variable \(j\), set \(\hat{\mathbf{\Delta}}_{j}=(\hat{\Delta}_{j}^{1}, \hat{\Delta}_{j}^{2})\) where \(\hat{\Delta}_{j}^{1}=\Phi^{-1}(\pi_{0j})\) and \(\hat{\Delta}_{j}^{2}=\Phi^{-1}(\pi_{0j}+\pi_{1j})\) with \(\pi_{0j}=\sum_{i=1}^{n}\frac{I(x_{ij}=0)}{n}\) and \(\pi_{1j}=\sum_{i=1}^{n}\frac{I(x_{ij}=1)}{n}\).
estimate$zratios
#> [[1]]
#> [1] NA
#> 
#> [[2]]
#> [1] 0.5
#> 
#> [[3]]
#> [1] 0.3 0.8
#> 
#> [[4]]
#> [1] 0.5
  • Compute \(F^{-1}(\hat{\tau}_{jk})\) as \(\hat{r}_{jk}=argmin\{F(r)-\hat{\tau}_{jk}\}^{2}\) solved via optimize function in R with accuracy tol.
estimate$Rpointwise
#>           [,1]      [,2]      [,3]      [,4]
#> [1,] 1.0000000 0.5529903 0.4480984 0.5826171
#> [2,] 0.5529903 1.0000000 0.4050223 0.5821513
#> [3,] 0.4480984 0.4050223 1.0000000 0.4653875
#> [4,] 0.5826171 0.5821513 0.4653875 1.0000000

Approximation method (method = "approx")

A faster approximation method is based on multi-linear interpolation of pre-computed inverse bridge function on a fixed grid of points (Yoon, Müller, and Gaynanova 2021). This is possible as the inverse bridge function is an analytic function of at most 5 parameters:

  • Kendall’s \(\tau\)
  • Proportion of zeros in the 1st variable
  • (Possibly) proportion of zeros and ones in the 1st variable
  • (Possibly) proportion of zeros in the 2nd variable
  • (Possibly) proportion of zeros and ones in the 2nd variable

In short, d-dimensional multi-linear interpolation uses a weighted average of \(2^{d}\) neighbors to approximate the function values at the points within the d-dimensional cube of the neighbors, and to perform interpolation, latentcor takes advantage of the R package chebpol (Gaure 2019). This approximation method has been first described in (Yoon, Müller, and Gaynanova 2021) for continuous/binary/truncated cases. In latentcor, we additionally implement ternary case, and optimize the choice of grid as well as interpolation boundary for faster computations with smaller memory footprint.

#estimate = latentcor(X, types = c("con", "bin", "ter", "tru"), method = "approx")

Algorithm for Approximation method

Input: Let \(\check{g}=h(g)\), pre-computed values \(F^{-1}(h^{-1}(\check{g}))\) on a fixed grid \(\check{g}\in\check{\cal{G}}\) based on the type of variables \(j\) and \(k\). For binary/continuous case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j})\); for binary/binary case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j}, \check{\Delta}_{k})\); for truncated/continuous case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j})\); for truncated/truncated case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j}, \check{\Delta}_{k})\); for ternary/continuous case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j}^{1}, \check{\Delta}_{j}^{2})\); for ternary/binary case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j}^{1}, \check{\Delta}_{j}^{2}, \check{\Delta}_{k})\); for ternary/truncated case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j}^{1}, \check{\Delta}_{j}^{2}, \check{\Delta}_{k})\); for ternay/ternary case, \(\check{g}=(\check{\tau}_{jk}, \check{\Delta}_{j}^{1}, \check{\Delta}_{j}^{2}, \check{\Delta}_{k}^{1}, \check{\Delta}_{k}^{2})\).

  • Step 1 and Step 2 same as Original method.

  • Step 3. If \(|\hat{\tau}_{jk}|\le \mbox{ratio}\times \bar{\tau}_{jk}(\cdot)\), apply interpolation; otherwise apply Original method.

To avoid interpolation in areas with high approximation errors close to the boundary, we use hybrid scheme in Step 3. The parameter ratio controls the size of the region where the interpolation is performed (ratio = 0 means no interpolation, ratio = 1 means interpolation is always performed). For the derivation of approximate bound for BC, BB, TC, TB, TT cases see Yoon, Müller, and Gaynanova (2021). The derivation of approximate bound for NC, NB, NN, NT case is in the Appendix.

\[ \bar{\tau}_{jk}(\cdot)= \begin{cases} 2\pi_{0j}(1-\pi_{0j}) & for \; BC \; case\\ 2\min(\pi_{0j},\pi_{0k})\{1-\max(\pi_{0j}, \pi_{0k})\} & for \; BB \; case\\ 2\{\pi_{0j}(1-\pi_{0j})+\pi_{1j}(1-\pi_{0j}-\pi_{1j})\} & for \; NC \; case\\ 2\min(\pi_{0j}(1-\pi_{0j})+\pi_{1j}(1-\pi_{0j}-\pi_{1j}),\pi_{0k}(1-\pi_{0k})) & for \; NB \; case\\ 2\min(\pi_{0j}(1-\pi_{0j})+\pi_{1j}(1-\pi_{0j}-\pi_{1j}), \\ \;\;\;\;\;\;\;\;\;\;\pi_{0k}(1-\pi_{0k})+\pi_{1k}(1-\pi_{0k}-\pi_{1k})) & for \; NN \; case\\ 1-(\pi_{0j})^{2} & for \; TC \; case\\ 2\max(\pi_{0k},1-\pi_{0k})\{1-\max(\pi_{0k},1-\pi_{0k},\pi_{0j})\} & for \; TB \; case\\ 1-\{\max(\pi_{0j},\pi_{0k},\pi_{1k},1-\pi_{0k}-\pi_{1k})\}^{2} & for \; TN \; case\\ 1-\{\max(\pi_{0j},\pi_{0k})\}^{2} & for \; TT \; case\\ \end{cases} \]

By default, latentcor uses ratio = 0.9 as this value was recommended in Yoon, Müller, and Gaynanova (2021) having a good balance of accuracy and computational speed. This value, however, can be modified by the user.

#latentcor(X, types = c("con", "bin", "ter", "tru"), method = "approx", ratio = 0.99)$R
#latentcor(X, types = c("con", "bin", "ter", "tru"), method = "approx", ratio = 0.4)$R
latentcor(X, types = c("con", "bin", "ter", "tru"), method = "original")$R
#>           [,1]      [,2]      [,3]      [,4]
#> [1,] 1.0000000 0.5524373 0.4476503 0.5820345
#> [2,] 0.5524373 1.0000000 0.4046173 0.5815691
#> [3,] 0.4476503 0.4046173 1.0000000 0.4649222
#> [4,] 0.5820345 0.5815691 0.4649222 1.0000000

The lower is the ratio, the closer is the approximation method to original method (with ratio = 0 being equivalent to method = "original"), but also the higher is the cost of computations.

library(microbenchmark)
#microbenchmark(latentcor(X, types = c("con", "bin", "ter", "tru"), method = "approx", ratio = 0.99)$R)
#microbenchmark(latentcor(X, types = c("con", "bin", "ter", "tru"), method = "approx", ratio = 0.4)$R)
microbenchmark(latentcor(X, types = c("con", "bin", "ter", "tru"), method = "original")$R)
#> Unit: milliseconds
#>                                                                        expr
#>  latentcor(X, types = c("con", "bin", "ter", "tru"), method = "original")$R
#>      min       lq    mean   median      uq     max neval
#>  29.6928 30.16525 30.8096 30.53385 31.0322 35.1031   100

Rescaled Grid for Interpolation

Since \(|\hat{\tau}|\le \bar{\tau}\), the grid does not need to cover the whole domain \(\tau\in[-1, 1]\). To optimize memory associated with storing the grid, we rescale \(\tau\) as follows: \(\check{\tau}_{jk}=\tau_{jk}/\bar{\tau}_{jk}\in[-1, 1]\), where \(\bar{\tau}_{jk}\) is as defined above.

In addition, for ternary variable \(j\), it always holds that \(\Delta_{j}^{2}>\Delta_{j}^{1}\) since \(\Delta_{j}^{1}=\Phi^{-1}(\pi_{0j})\) and \(\Delta_{j}^{2}=\Phi^{-1}(\pi_{0j}+\pi_{1j})\). Thus, the grid should not cover the the area corresponding to \(\Delta_{j}^{2}\le\Delta_{j}^{1}\). We thus rescale as follows: \(\check{\Delta}_{j}^{1}=\Delta_{j}^{1}/\Delta_{j}^{2}\in[0, 1]\); \(\check{\Delta}_{j}^{2}=\Delta_{j}^{2}\in[0, 1]\).

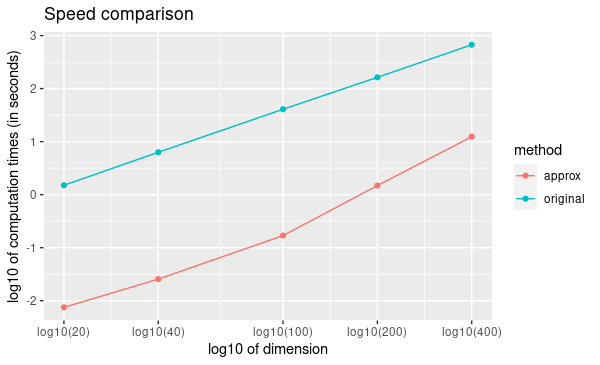
Speed Comparison

To illustrate the speed improvement by method = "approx", we plot the run time scaling behavior of method = "approx" and method = "original" (setting types for gen_data by replicating c("con", "bin", "ter", "tru") multiple times) with increasing dimensions \(p = [20, 40, 100, 200, 400]\) at sample size \(n = 100\) using simulation data. Figure below summarizes the observed scaling in a log-log plot. For both methods we observe the expected \(O(p^2)\) scaling behavior with dimension p, i.e., a linear scaling in the log-log plot. However, method = "approx" is at least one order of magnitude faster than method = "original" independent of the dimension of the problem.

Adjustment of pointwise-estimator for positive-definiteness

Since the estimation is performed point-wise, the resulting matrix of estimated latent correlations is not guaranteed to be positive semi-definite. For example, this could be expected when the sample size is small (and so the estimation error for each pairwise correlation is larger)

set.seed("234820")
X = gen_data(n = 6, types = c("con", "bin", "ter", "tru"))$X
X
#>            [,1] [,2] [,3]      [,4]
#> [1,] -0.5182800    0    1 0.1021738
#> [2,] -1.3017092    0    0 0.0000000
#> [3,]  0.3145191    1    2 0.4213514
#> [4,] -0.6093291    0    1 1.2771610
#> [5,] -1.3175490    1    0 0.0000000
#> [6,] -0.7807245    1    1 0.0000000
out = latentcor(X, types = c("con", "bin", "ter", "tru"))
out$Rpointwise
#>            [,1]       [,2]      [,3]       [,4]
#> [1,]  1.0000000 -0.1477240 0.9990000  0.8548518
#> [2,] -0.1477240  1.0000000 0.3523666 -0.5030324
#> [3,]  0.9990000  0.3523666 1.0000000  0.9114307
#> [4,]  0.8548518 -0.5030324 0.9114307  1.0000000
eigen(out$Rpointwise)$values
#> [1]  2.85954424  1.29130852  0.09944544 -0.25029820

latentcor automatically corrects the pointwise estimator to be positive definite by making two adjustments. First, if Rpointwise has smallest eigenvalue less than zero, the latentcor projects this matrix to the nearest positive semi-definite matrix. The user is notified of this adjustment through the message (supressed in previous code chunk), e.g.

out = latentcor(X, types = c("con", "bin", "ter", "tru"))

Second, latentcor shrinks the adjusted matrix of correlations towards identity matrix using the parameter \(\nu\) with default value of 0.001 (nu = 0.001), so that the resulting R is strictly positive definite with the minimal eigenvalue being greater or equal to \(\nu\). That is \[ R = (1 - \nu) \widetilde R + \nu I, \] where \(\widetilde R\) is the nearest positive semi-definite matrix to Rpointwise.

out = latentcor(X, types = c("con", "bin", "ter", "tru"), nu = 0.001)
out$Rpointwise
#>            [,1]       [,2]      [,3]       [,4]
#> [1,]  1.0000000 -0.1477240 0.9990000  0.8548518
#> [2,] -0.1477240  1.0000000 0.3523666 -0.5030324
#> [3,]  0.9990000  0.3523666 1.0000000  0.9114307
#> [4,]  0.8548518 -0.5030324 0.9114307  1.0000000
out$R
#>            [,1]       [,2]      [,3]       [,4]
#> [1,]  1.0000000 -0.1053533 0.9232992  0.9048072
#> [2,] -0.1053533  1.0000000 0.2372115 -0.4244433
#> [3,]  0.9232992  0.2372115 1.0000000  0.7723678
#> [4,]  0.9048072 -0.4244433 0.7723678  1.0000000

As a result, R and Rpointwise could be quite different when sample size \(n\) is small. When \(n\) is large and \(p\) is moderate, the difference is typically driven by parameter nu.

set.seed("234820")
X = gen_data(n = 100, types = c("con", "bin", "ter", "tru"))$X
out = latentcor(X, types = c("con", "bin", "ter", "tru"), nu = 0.001)
out$Rpointwise
#>           [,1]      [,2]      [,3]      [,4]
#> [1,] 1.0000000 0.5528213 0.4476819 0.5823120
#> [2,] 0.5528213 1.0000000 0.4058967 0.5808889
#> [3,] 0.4476819 0.4058967 1.0000000 0.4567771
#> [4,] 0.5823120 0.5808889 0.4567771 1.0000000
out$R
#>           [,1]      [,2]      [,3]      [,4]
#> [1,] 1.0000000 0.5522684 0.4472342 0.5817297
#> [2,] 0.5522684 1.0000000 0.4054908 0.5803080
#> [3,] 0.4472342 0.4054908 1.0000000 0.4563203
#> [4,] 0.5817297 0.5803080 0.4563203 1.0000000

Appendix

Derivation of bridge function \(F\) for ternary/truncated case

Without loss of generality, let \(j=1\) and \(k=2\). By the definition of Kendall’s \(\tau\), \[ \tau_{12}=E(\hat{\tau}_{12})=E[\frac{2}{n(n-1)}\sum_{1\leq i\leq i' \leq n} sign\{(X_{i1}-X_{i'1})(X_{i2}-X_{i'2})\}]. \] Since \(X_{1}\) is ternary, \[\begin{align} &sign(X_{1}-X_{1}') \nonumber\\ =&[I(U_{1}>C_{11},U_{1}'\leq C_{11})+I(U_{1}>C_{12},U_{1}'\leq C_{12})-I(U_{1}>C_{12},U_{1}'\leq C_{11})] \nonumber\\ &-[I(U_{1}\leq C_{11}, U_{1}'>C_{11})+I(U_{1}\leq C_{12}, U_{1}'>C_{12})-I(U_{1}\leq C_{11}, U_{1}'>C_{12})] \nonumber\\ =&[I(U_{1}>C_{11})-I(U_{1}>C_{11},U_{1}'>C_{11})+I(U_{1}>C_{12})-I(U_{1}>C_{12},U_{1}'>C_{12}) \nonumber\\ &-I(U_{1}>C_{12})+I(U_{1}>C_{12},U_{1}'>C_{11})] \nonumber\\ &-[I(U_{1}'>C_{11})-I(U_{1}>C_{11},U_{1}'>C_{11})+I(U_{1}'>C_{12})-I(U_{1}>C_{12},U_{1}'>C_{12}) \nonumber\\ &-I(U_{1}'>C_{12})+I(U_{1}>C_{11},U_{1}'>C_{12})] \nonumber\\ =&I(U_{1}>C_{11})+I(U_{1}>C_{12},U_{1}'>C_{11})-I(U_{1}'>C_{11})-I(U_{1}>C_{11},U_{1}'>C_{12}) \nonumber\\ =&I(U_{1}>C_{11},U_{1}'\leq C_{12})-I(U_{1}'>C_{11},U_{1}\leq C_{12}). \end{align}\] Since \(X_{2}\) is truncated, \(C_{1}>0\) and \[\begin{align} sign(X_{2}-X_{2}')=&-I(X_{2}=0,X_{2}'>0)+I(X_{2}>0,X_{2}'=0) \nonumber\\ &+I(X_{2}>0,X_{2}'>0)sign(X_{2}-X_{2}') \nonumber\\ =&-I(X_{2}=0)+I(X_{2}'=0)+I(X_{2}>0,X_{2}'>0)sign(X_{2}-X_{2}'). \end{align}\] Since \(f\) is monotonically increasing, \(sign(X_{2}-X_{2}')=sign(Z_{2}-Z_{2}')\), \[\begin{align} \tau_{12}=&E[I(U_{1}>C_{11},U_{1}'\leq C_{12}) sign(X_{2}-X_{2}')] \nonumber\\ &-E[I(U_{1}'>C_{11},U_{1}\leq C_{12}) sign(X_{2}-X_{2}')] \nonumber\\ =&-E[I(U_{1}>C_{11},U_{1}'\leq C_{12}) I(X_{2}=0)] \nonumber\\ &+E[I(U_{1}>C_{11},U_{1}'\leq C_{12}) I(X_{2}'=0)] \nonumber\\ &+E[I(U_{1}>C_{11},U_{1}'\leq C_{12})I(X_{2}>0,X_{2}'>0)sign(Z_{2}-Z_{2}')] \nonumber\\ &+E[I(U_{1}'>C_{11},U_{1}\leq C_{12}) I(X_{2}=0)] \nonumber\\ &-E[I(U_{1}'>C_{11},U_{1}\leq C_{12}) I(X_{2}'=0)] \nonumber\\ &-E[I(U_{1}'>C_{11},U_{1}\leq C_{12})I(X_{2}>0,X_{2}'>0)sign(Z_{2}-Z_{2}')] \nonumber\\ =&-2E[I(U_{1}>C_{11},U_{1}'\leq C_{12}) I(X_{2}=0)] \nonumber\\ &+2E[I(U_{1}>C_{11},U_{1}'\leq C_{12}) I(X_{2}'=0)] \nonumber\\ &+E[I(U_{1}>C_{11},U_{1}'\leq C_{12})I(X_{2}>0,X_{2}'>0)sign(Z_{2}-Z_{2}')] \nonumber\\ &-E[I(U_{1}'>C_{11},U_{1}\leq C_{12})I(X_{2}>0,X_{2}'>0)sign(Z_{2}-Z_{2}')]. \end{align}\] From the definition of \(U\), let \(Z_{j}=f_{j}(U_{j})\) and \(\Delta_{j}=f_{j}(C_{j})\) for \(j=1,2\). Using \(sign(x)=2I(x>0)-1\), we obtain \[\begin{align} \tau_{12}=&-2E[I(Z_{1}>\Delta_{11},Z_{1}'\leq \Delta_{12},Z_{2}\leq \Delta_{2})]+2E[I(Z_{1}>\Delta_{11},Z_{1}'\leq \Delta_{12},Z_{2}'\leq \Delta_{2})] \nonumber\\ &+2E[I(Z_{1}>\Delta_{11},Z_{1}'\leq \Delta_{12})I(Z_{2}>\Delta_{2},Z_{2}'>\Delta_{2},Z_{2}-Z_{2}'>0)] \nonumber\\ &-2E[I(Z_{1}'>\Delta_{11},Z_{1}\leq \Delta_{12})I(Z_{2}>\Delta_{2},Z_{2}'>\Delta_{2},Z_{2}-Z_{2}'>0)] \nonumber\\ =&-2E[I(Z_{1}>\Delta_{11},Z_{1}'\leq \Delta_{12}, Z_{2}\leq \Delta_{2})]+2E[I(Z_{1}>\Delta_{11},Z_{1}'\leq \Delta_{12}, Z_{2}'\leq \Delta_{2})] \nonumber\\ &+2E[I(Z_{1}>\Delta_{11},Z_{1}'\leq\Delta_{12},Z_{2}'>\Delta_{2},Z_{2}>Z_{2}')] \nonumber\\ &-2E[I(Z_{1}'>\Delta_{11},Z_{1}\leq\Delta_{12},Z_{2}'>\Delta_{2},Z_{2}>Z_{2}')]. \end{align}\] Since \(\{\frac{Z_{2}'-Z_{2}}{\sqrt{2}}, -Z{1}\}\), \(\{\frac{Z_{2}'-Z_{2}}{\sqrt{2}}, Z{1}'\}\) and \(\{\frac{Z_{2}'-Z_{2}}{\sqrt{2}}, -Z{2}'\}\) are standard bivariate normally distributed variables with correlation \(-\frac{1}{\sqrt{2}}\), \(r/\sqrt{2}\) and \(-\frac{r}{\sqrt{2}}\), respectively, by the definition of \(\Phi_3(\cdot,\cdot, \cdot;\cdot)\) and \(\Phi_4(\cdot,\cdot, \cdot,\cdot;\cdot)\) we have \[\begin{align} F_{NT}(r;\Delta_{j}^{1},\Delta_{j}^{2},\Delta_{k})= & -2\Phi_{3}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},\Delta_{k};\begin{pmatrix} 1 & 0 & -r \\ 0 & 1 & 0 \\ -r & 0 & 1 \end{pmatrix} \right\} \nonumber\\ &+2\Phi_{3}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},\Delta_{k};\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & r \\ 0 & r & 1 \end{pmatrix}\right\}\nonumber \\ & +2\Phi_{4}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k},0;\begin{pmatrix} 1 & 0 & 0 & \frac{r}{\sqrt{2}} \\ 0 & 1 & -r & \frac{r}{\sqrt{2}} \\ 0 & -r & 1 & -\frac{1}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & \frac{r}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 1 \end{pmatrix}\right\} \nonumber\\ &-2\Phi_{4}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k},0;\begin{pmatrix} 1 & 0 & r & -\frac{r}{\sqrt{2}} \\ 0 & 1 & 0 & -\frac{r}{\sqrt{2}} \\ r & 0 & 1 & -\frac{1}{\sqrt{2}} \\ -\frac{r}{\sqrt{2}} & -\frac{r}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 1 \end{pmatrix}\right\}. \end{align}\] Using the facts that \[\begin{align} &\Phi_{4}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k},0;\begin{pmatrix} 1 & 0 & r & -\frac{r}{\sqrt{2}} \\ 0 & 1 & 0 & -\frac{r}{\sqrt{2}} \\ r & 0 & 1 & -\frac{1}{\sqrt{2}} \\ -\frac{r}{\sqrt{2}} & -\frac{r}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 1 \end{pmatrix}\right\} \nonumber\\ &+\Phi_{4}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k},0;\begin{pmatrix} 1 & 0 & r & \frac{r}{\sqrt{2}} \\ 0 & 1 & 0 & \frac{r}{\sqrt{2}} \\ r & 0 & 1 & \frac{1}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & \frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 1 \end{pmatrix}\right\} \nonumber\\ =&\Phi_{3}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k};\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & r \\ 0 & r & 1 \end{pmatrix}\right\} \end{align}\] and \[\begin{align} &\Phi_{3}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k};\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & r \\ 0 & r & 1 \end{pmatrix}\right\}+\Phi_{3}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},\Delta_{k};\begin{pmatrix} 1 & 0 & -r \\ 0 & 1 & 0 \\ -r & 0 & 1 \end{pmatrix} \right\} \nonumber\\ =&\Phi_{2}(-\Delta_{j}^{1},\Delta_{j}^{2};0) =\Phi(-\Delta_{j}^{1})\Phi(\Delta_{j}^{2}). \end{align}\] So that, \[\begin{align} F_{NT}(r;\Delta_{j}^{1},\Delta_{j}^{2},\Delta_{k})= & -2\Phi(-\Delta_{j}^{1})\Phi(\Delta_{j}^{2}) \nonumber\\ &+2\Phi_{3}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},\Delta_{k};\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & r \\ 0 & r & 1 \end{pmatrix}\right\}\nonumber \\ & +2\Phi_{4}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k},0;\begin{pmatrix} 1 & 0 & 0 & \frac{r}{\sqrt{2}} \\ 0 & 1 & -r & \frac{r}{\sqrt{2}} \\ 0 & -r & 1 & -\frac{1}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & \frac{r}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 1 \end{pmatrix}\right\} \nonumber\\ &+2\Phi_{4}\left\{-\Delta_{j}^{1},\Delta_{j}^{2},-\Delta_{k},0;\begin{pmatrix} 1 & 0 & r & \frac{r}{\sqrt{2}} \\ 0 & 1 & 0 & \frac{r}{\sqrt{2}} \\ r & 0 & 1 & \frac{1}{\sqrt{2}} \\ \frac{r}{\sqrt{2}} & \frac{r}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 1 \end{pmatrix}\right\}. \end{align}\]

It is easy to get the bridge function for truncated/ternary case by switching \(j\) and \(k\).

Derivation of approximate bound for the ternary/continuous case

Let \(n_{0x}=\sum_{i=1}^{n_x}I(x_{i}=0)\), \(n_{2x}=\sum_{i=1}^{n_x}I(x_{i}=2)\), \(\pi_{0x}=\frac{n_{0x}}{n_{x}}\) and \(\pi_{2x}=\frac{n_{2x}}{n_{x}}\), then \[\begin{align} |\tau(\mathbf{x})|\leq & \frac{n_{0x}(n-n_{0x})+n_{2x}(n-n_{0x}-n_{2x})}{\begin{pmatrix} n \\ 2 \end{pmatrix}} \nonumber\\ = & 2\{\frac{n_{0x}}{n-1}-(\frac{n_{0x}}{n})(\frac{n_{0x}}{n-1})+\frac{n_{2x}}{n-1}-(\frac{n_{2x}}{n})(\frac{n_{0x}}{n-1})-(\frac{n_{2x}}{n})(\frac{n_{2x}}{n-1})\} \nonumber\\ \approx & 2\{\frac{n_{0x}}{n}-(\frac{n_{0x}}{n})^2+\frac{n_{2x}}{n}-(\frac{n_{2x}}{n})(\frac{n_{0x}}{n})-(\frac{n_{2x}}{n})^2\} \nonumber\\ = & 2\{\pi_{0x}(1-\pi_{0x})+\pi_{2x}(1-\pi_{0x}-\pi_{2x})\} \end{align}\]

For ternary/binary and ternary/ternary cases, we combine the two individual bounds.

Derivation of approximate bound for the ternary/truncated case

Let \(\mathbf{x}\in\mathcal{R}^{n}\) and \(\mathbf{y}\in\mathcal{R}^{n}\) be the observed \(n\) realizations of ternary and truncated variables, respectively. Let \(n_{0x}=\sum_{i=0}^{n}I(x_{i}=0)\), \(\pi_{0x}=\frac{n_{0x}}{n}\), \(n_{1x}=\sum_{i=0}^{n}I(x_{i}=1)\), \(\pi_{1x}=\frac{n_{1x}}{n}\), \(n_{2x}=\sum_{i=0}^{n}I(x_{i}=2)\), \(\pi_{2x}=\frac{n_{2x}}{n}\), \(n_{0y}=\sum_{i=0}^{n}I(y_{i}=0)\), \(\pi_{0y}=\frac{n_{0y}}{n}\), \(n_{0x0y}=\sum_{i=0}^{n}I(x_{i}=0 \;\& \; y_{i}=0)\), \(n_{1x0y}=\sum_{i=0}^{n}I(x_{i}=1 \;\& \; y_{i}=0)\) and \(n_{2x0y}=\sum_{i=0}^{n}I(x_{i}=2 \;\& \; y_{i}=0)\) then \[\begin{align} |\tau(\mathbf{x}, \mathbf{y})|\leq & \frac{\begin{pmatrix}n \\ 2\end{pmatrix}-\begin{pmatrix}n_{0x} \\ 2\end{pmatrix}-\begin{pmatrix}n_{1x} \\ 2\end{pmatrix}-\begin{pmatrix} n_{2x} \\ 2 \end{pmatrix}-\begin{pmatrix}n_{0y} \\ 2\end{pmatrix}+\begin{pmatrix}n_{0x0y} \\ 2 \end{pmatrix}+\begin{pmatrix}n_{1x0y} \\ 2\end{pmatrix}+\begin{pmatrix}n_{2x0y} \\ 2\end{pmatrix}}{\begin{pmatrix}n \\ 2\end{pmatrix}} \nonumber \end{align}\] Since \(n_{0x0y}\leq\min(n_{0x},n_{0y})\), \(n_{1x0y}\leq\min(n_{1x},n_{0y})\) and \(n_{2x0y}\leq\min(n_{2x},n_{0y})\) we obtain \[\begin{align} |\tau(\mathbf{x}, \mathbf{y})|\leq & \frac{\begin{pmatrix}n \\ 2\end{pmatrix}-\begin{pmatrix}n_{0x} \\ 2\end{pmatrix}-\begin{pmatrix}n_{1x} \\ 2\end{pmatrix}-\begin{pmatrix} n_{2x} \\ 2 \end{pmatrix}-\begin{pmatrix}n_{0y} \\ 2\end{pmatrix}}{\begin{pmatrix}n \\ 2\end{pmatrix}} \nonumber\\ & + \frac{\begin{pmatrix}\min(n_{0x},n_{0y}) \\ 2 \end{pmatrix}+\begin{pmatrix}\min(n_{1x},n_{0y}) \\ 2\end{pmatrix}+\begin{pmatrix}\min(n_{2x},n_{0y}) \\ 2\end{pmatrix}}{\begin{pmatrix}n \\ 2\end{pmatrix}} \nonumber\\ \leq & \frac{\begin{pmatrix}n \\ 2\end{pmatrix}-\begin{pmatrix}\max(n_{0x},n_{1x},n_{2x},n_{0y}) \\ 2\end{pmatrix}}{\begin{pmatrix}n \\ 2\end{pmatrix}} \nonumber\\ \leq & 1-\frac{\max(n_{0x},n_{1x},n_{2x},n_{0y})(\max(n_{0x},n_{1x},n_{2x},n_{0y})-1)}{n(n-1)} \nonumber\\ \approx & 1-(\frac{\max(n_{0x},n_{1x},n_{2x},n_{0y})}{n})^{2} \nonumber\\ =& 1-\{\max(\pi_{0x},\pi_{1x},\pi_{2x},\pi_{0y})\}^{2} \nonumber\\ =& 1-\{\max(\pi_{0x},(1-\pi_{0x}-\pi_{2x}),\pi_{2x},\pi_{0y})\}^{2} \end{align}\]

It is easy to get the approximate bound for truncated/ternary case by switching \(\mathbf{x}\) and \(\mathbf{y}\).

References

Croux, Christophe, Peter Filzmoser, and Heinrich Fritz. 2013. “Robust Sparse Principal Component Analysis.” Technometrics 55 (2): 202–14.
Fan, Jianqing, Han Liu, Yang Ning, and Hui Zou. 2017. “High Dimensional Semiparametric Latent Graphical Model for Mixed Data.” Journal of the Royal Statistical Society. Series B: Statistical Methodology 79 (2): 405–21.
Filzmoser, Peter, Heinrich Fritz, and Klaudius Kalcher. 2021. pcaPP: Robust PCA by Projection Pursuit. https://CRAN.R-project.org/package=pcaPP.
Fox, John. 2019. Polycor: Polychoric and Polyserial Correlations. https://CRAN.R-project.org/package=polycor.
Gaure, Simen. 2019. Chebpol: Multivariate Interpolation. https://github.com/sgaure/chebpol.
Liu, Han, John Lafferty, and Larry Wasserman. 2009. “The Nonparanormal: Semiparametric Estimation of High Dimensional Undirected Graphs.” Journal of Machine Learning Research 10 (10).
Quan, Xiaoyun, James G Booth, and Martin T Wells. 2018. “Rank-Based Approach for Estimating Correlations in Mixed Ordinal Data.” arXiv Preprint arXiv:1809.06255.
Yoon, Grace, Raymond J Carroll, and Irina Gaynanova. 2020. “Sparse Semiparametric Canonical Correlation Analysis for Data of Mixed Types.” Biometrika 107 (3): 609–25.
Yoon, Grace, Christian L Müller, and Irina Gaynanova. 2021. “Fast Computation of Latent Correlations.” Journal of Computational and Graphical Statistics, 1–8.